УДК 378.147
В.П. Кайдан
старший викладач, кваліфікаційна категорія «спеціаліст вищої категорії»
Університет економіки і підприємництва
ORCID: 0000-0003-2008-3539
ВИКОРИСТАННЯ СИСТЕМИ КОМП’ЮТЕРНОЇ МАТЕМАТИКИ MAPLE ПРИ РОЗВ’ЯЗУВАННІ ЗАДАЧ ФІЗИЧНОГО ЗМІСТУ
У статті висвітлено сучасний стан використання систем комп’ютерної математики, наведено переваги використання системи комп’ютерної математики Maple, обґрунтовано можливість та доцільність використання системи комп’ютерної математики Maple під час розв’язування фізичних задач, визначено перспективні напрямки подальших досліджень.
Ключові слова: система комп’ютерної математики, природничо-математичні дисципліни, розв’язування задач, математичні розрахунки в фізиці, Maple.
V.P. Kaidan
University of Economics and Entrepreneurship
THE USE OF THE MAPLE COMPUTER MATHEMATICS SYSTEM IN SOLVING PROBLEMS OF PHYSICAL CONTENT
The article describes the current state of the use of computer mathematics systems, the advantages of using the Maple computer mathematics system, the possibility and relevance of using the Maple computer mathematics system in solving physical problems are proved, and the promising areas for further research are identified.
Keywords: computer mathematics system, natural and mathematical disciplines, problem solving, mathematical calculations in physics, Maple.
Постановка проблеми в загальному вигляді.
Поняття сучасного фахівця не можна уявити без таких якості, як швидка реакція на будь-які зміни в оточуючому його середовищі. Крім самої реакції, потрібні навички аналізу виникнення цих змін, відокремлювання позитивних та негативних факторів, уміння передбачати наслідки, обирати найбільш ефективну стратегію поведінки – саме ці уміння, окрім особистих якостей, дозволяють вважати людину ефективним й конкурентоспроможним працівником.
Розвиток таких якостей може займати багато років, але найбільш доцільним є активізація цього процесу саме в період отримання освіти. Це зумовлено певною концентрацією уваги на відносно обмеженому колі питань порівняно із звичайним життям, можливістю отримання кваліфікованої допомоги від викладачів під час навчання та фахівців під час проходження практики на підприємстві, можливістю діагностики результатів навчання та, якщо виникла потреба, здійсненні корекції для усунення недоліків із опанування як конкретних навичок, так і розуміння тем та розділів навчальних дисциплін.
Таким чином, під час навчального процесу доцільно використовувати засоби що зменшують час на будь-яку «механічну роботу» – діяльність, яка не несе можливостей зростання творчих якостей. Одним з таких засобів є системи комп’ютерної математики, що дозволяють користувачеві під час розв’язання математичних, фізичних, статистичних, економічних задач та задач з інших галузей мінімізувати час потрібний для проведення математичних розрахунків й приділити основну увагу аналізу отриманих результатів та синтезу найбільш оптимального рішення.
Аналіз досліджень і публікацій.
Проблеми впровадження систем комп’ютерної математики у навчальний процес розглядалися багатьма науковцями, зокрема, Н.Л Сосницькою, М.Л. Жалдаком, В.Ф. Заболотним [1,2,6]. Питанням автоматизації процесу обчислень під час розв’язування задач з фізики та впровадженням використання комп’ютерного моделювання у навчальний процес займалися М.Б .Ковальчук, О.Е. Корнійчук, І.Р. Мілюкова, К.Г. Чорнобай. [4,5,7] Однак, навіть існуючий на даний час значний обсяг напрацювань теоретичного та прикладного матеріалу не дозволяє на всіх етапах навчального процесу залучати системи комп’ютерної математики до розв’язування завдань з достатньою ефективністю. Що, в свою чергу, підкреслює актуальність цієї проблеми.
Формулювання мети статті. У даній статті автором наводиться обґрунтування необхідності впровадження систем комп‘ютерної математики в навчальний процес в аспекті потреби більш раціонального використання часу. Розглянуто приклад використання системи комп’ютерної математики Maple як демонстрацію можливостей її використання в освітньому процесі, зокрема, під час розв’язування задач з фізики.
Виклад основного матеріалу.
Результати будь-якої професійної діяльності залежать не тільки від особистих якостей працівника, але й від використовуваного ним технічного оснащення – чим більш високотехнологічне оснащення використовується, тим більш ефективною є праця, тим кращий результат. Питання якості стосується в даному випадку не тільки самих приладів й устаткування, але й можливості використовувати сучасне програмне забезпечення, що відповідає вимогам, є надійним, дозволяє скорочувати час, який витрачається на обробку інформації. Особливо актуальним це питання є для спеціальностей, професійна діяльність яких пов’язана з великою кількістю однотипних математичних розрахунків. Навіть, якщо їх складність не створює проблем, обробка статистичних даних з великою кількістю числових значень здатна зайняти значний проміжок часу. В результаті – час, який можна витратити на аналіз результатів, створення нових ідей або формулювання гіпотез, прийняття рішень щодо актуальності впровадження подальших змін в процесах суттєво скорочується. А це, в свою чергу, негативно впливає на результати діяльності.
На даний час вже існує велика кількість програмних пакетів, що є придатними для розв’язування прикладних задач з багатьох галузей. Крім того, ці засоби в сукупності із інформаційними технологіями, що застосовуються для їх реалізації, є гарним доповненням до навчального процесу. Під системами комп’ютерної математики розуміють засоби, що автоматизують виконання чисельних і аналітичних обчислень. За їх допомогою суттєво спрощуються обчислення під час розв’язання великої кількості наукових та професійних задач, отримання навичок при опрацюванні навчального матеріалу за допомогою наочної візуалізації як початкових даних, так й результатів обчислень. Крім того, їх можна використовувати як довідники з математичних обчислень. [3]
Останні десятиліття принесли нам появу багатьох універсальних математичних пакетів, серед яких можна зазначити Derive, MathCad, MathLab, Maple, Mathematica, MuPad. Всі вони характеризуються наявністю зручного та зрозумілого користувачеві інтерфейсу, реалізацією значної кількості стандартних та спеціальних математичних операцій та функцій, наявністю потужних графічних засобів дво- та тривимірної графіки, наявністю власних мов програмування та засобів підготовки математичних текстів для друку. Особливо зручно й важливо для навчальних цілей те, що є можливість експортувати дані в інші програмні продукти та імпортувати з них даних для подальшого опрацювання.
Слід зазначити, що здебільшого проблеми під час виконання завдань з фізики, математики та інших дисциплін виникають саме через використання відносно складного математичного апарату. Особливо під час роботи з громіздкими формулами, результат яких потрібно отримати як наближене значення. Такий процес призводить до втрати практичної значущості самого розв’язку завдання, оскільки основна увага приділяється лише правильному застосуванню математичних методів та дотриманню послідовності етапів самої методики розрахунків. У противагу цьому, застосування будь-якої системи комп’ютерної математики у навчальному процесі при вивченні дисциплін природничо-математичного спрямування, технічних або економічних дисциплін значно спрощує сам процес отримання результату, головним чином суттєво скорочуючи час. Потужні можливості графіки та засоби візуального програмування особливо допомагають під час використання професійних знань на основі законів фізики, оскільки дозволяють візуалізувати результати обчислень. Це має велике значення, оскільки здебільшого здобувачі освіти мають відносно слабкі практичні навички з аналізу функцій та побудови графіків, що є обов’язковим елементом під час розв’язування завдань пов’язаних з описом процесів. Крім того, знаходження похідних, обчислення інтегралів, розв’язування диференціальних рівнянь також, здебільшого, створюють значні проблеми для більшості студентів. Якщо ці навички не пов’язані з майбутньою професійною діяльністю й суттєво не впливають на розуміння технологічних або економічних процесів, то більш доцільно використовувати засоби комп’ютерної математики, які дозволяють виконувати необідні обчислення в автоматичному режимі з мінімальною витратою часу. Крім зазначеного вище, великою перевагою використання систем комп’ютерної математики є полегшення процесу опрацювання отриманих розрахунків, можливість їх редагувати, зберігання для подальшого спільного використання й, відповідно, можливого обговорення з посиланням на теоретичні дані, особливо в умовах дистанційного навчання. [5]
Серед багатьох ефективних систем комп’ютерної математики зосередимось на використанні Maple, яка на сьогоднішній день є одною із провідних обчислювальних систем комп’ютерної математики. Maple являє собою комплекс пакетів, кожен з яких має власну «спеціалізацію» й направлений на розв’язування завдань певного напрямку: лінійної алгебри, аналітичної геометрії, математичного аналізу, диференціальних рівнянь, математичної статистики, лінійного та нелінійного програмування тощо.
Традиційно, Maple вважають системою аналітико-символьних обчислень, що означає, що ця система в більшості випадків надає відповідь під час розв’язування завдань в символьному (аналітичному) вигляді. Maple – інтегрована система, що об’єднує в собі потужний язик програмування, заснований на мові С++ (мова для інтерактивного спілкування), редактор для підготовки та редагування документів і програм, сучасний багатовіконний користувацький інтерфейс, який надає можливість роботи в діалоговому режимі, глосарій, довідкову систему, ядро алгоритмів і правил символьних і аналітичних перетворень математичних виразів, числові та символьні процесори, систему діагностики помилок при обчисленні та перетвореннях, бібліотеку вбудованих і додаткових процедур і функцій, пакети зовнішніх функцій для розв’язування різного виду задач та підтримки інших мов програмування. [4]
Для наочної демонстрації можливостей системи комп’ютерної математики Maple під час розв’язування практичних задач з навчальної дисципліни «Фізика» розглянемо наступний приклад.
Вздовж координатної осі рухаються дві матеріальні точки. Їх рух описується наступними рівняннями: та
, де t – час руху.
Знайти час та координату точки їх зустрічі, якщо відомі значення параметрів:
.
Розв’язок:
Якщо розглядаємо зустріч двох тіл, то це означає, що в певний момент часу виконується рівність .
Таким чином отримаємо:
Звідки, в свою чергу, отримаємо:
Підставимо згідно вихідних даних значення параметрів в рівняння:
Знайдемо розв’язки отриманого квадратного рівняння:
Значення нам не підходить, оскільки час спостереження не може бути від’ємним числом. Таким чином, тіла зустрінуться через 1 секунду після початку руху.
Використовуємо рівняння руху однієї з точок для знаходження координати точки зустрічі:
Відповідь: тіла зустрінуться в точці з координатою 10.
За допомогою Maple розв’язок можна отримати наступним чином: або знайти розв’язки системи рівнянь, створеної з рівнянь, що описують рух тіл ( та
, враховуючи
), або побудувати графіки двох функцій
й визначити точку перетину цих графіків. Реалізація цих способів зображена на рисунку 1.
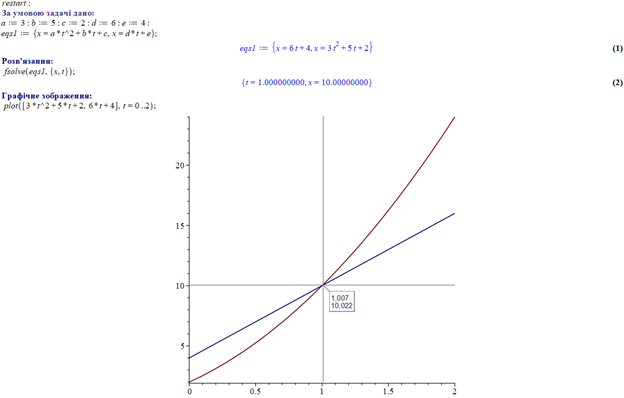
Рис. 1 Розв’язання задачі на рух двох тіл за допомогою Maple
За допомогою команди Maple відкриваємо нову сесію. Для того, щоб привласнити ім’я якомусь числу або функції, використовується оператор присвоювання «:=», що складається з двокрапки та знаку рівності. Математичному виразу, над яким будуть проводитися перетворення, можна присвоїти ім’я eqs1. Для наближеного розв’язання рівнянь використовується команда
. У разі раціонального рівняння
виводить весь список дійсних коренів. Скористаємось командою
для побудови графіка.
Слід зауважити, що під час аналізу графічного зображення, слід пам’ятати, що значення координат відображується з певною похибкою, що також можна побачити на рисунку.
Висновки та перспективи подальших досліджень у цьому напрямі.
Використання системи комп‘ютерної математики Maple дає змогу суттєво зменшити час, що витрачається на проведення математичних розрахунків під час розв’язання завдань різного рівня складності як під час аудиторних занять, так і при самостійному опрацюванні, сприяє більш глибокому розумінню фізичних законів і явищ завдяки можливостям візуалізації результатів та моделювання процесів, сприяє отриманню навичок аналізу та пошуку оптимальних шляхів розв’язку. В цілому, це підвищує зацікавленість студентів до вивчення дисциплін природничо-математичного та професійного спрямування, покращує результати навчальних досягнень. Наші подальші дослідження спрямовані на розробку методики використання системи комп‘ютерної математики Maple під час розв’язування задач професійної спрямованості з метою формування у студентів єдиної фізичної картини світу та поглибленню розуміння взаємозв’язку теоретичного матеріалу та практичних навичок професійного спрямування.
Список використаних джерел
- Жалдак, М. І. (2003). КОМП’ЮТЕР НА УРОКАХ МАТЕМАТИКИ: ПОСІБНИК ДЛЯ ВЧИТЕЛІВ. К.: РННЦ «Дініт».
- Заболотний, В. Ф. (2006). ВИКОРИСТАННЯ ДЕМОНСТРАЦІЙНИХ КОМП’ЮТЕРНИХ МОДЕЛЕЙ ПРИ НАВЧАННІ МЕТОДИКИ ВИВЧЕННЯ ХВИЛЬОВОЇ ОПТИКИ. Збірник наукових праць Кам’янець-Подільського національного університету імені Івана Огієнка. Серія педагогічна, 12, 110-113.
- Кайдан, В. П. & Кайдан Н. В. (2014). КОМП’ЮТЕРНІ ТЕХНОЛОГІЇ ЯК КОМПОНЕНТ ПРОЦЕСУ ВИКЛАДАННЯ ПРИРОДНИЧО-МАТЕМАТИЧНИХ ДИСЦИПЛІН. Гуманізація навчально-виховного процесу: збірник наукових праць, LXX(ІІ), 24-30.
- Ковальчук, М. Б. (2019). МОДЕЛЮВАННЯ ЗАДАЧ МАТЕМАТИЧНОЇ ФІЗИКИ В СИСТЕМІ КОМП’ЮТЕРНОЇ МАТЕМАТИКИ MAPLE. Фізико-математична освіта, 2(20), 40-47. https://doi.org/10.31110/2413-1571-2019-020-2-007
- Корнійчук, О. Е. (2016). ВИВЧЕННЯ ПОХІДНОЇ РАЗОМ ІЗ MAPLE. Фізико-математична освіта, 3(9), 61-69. https://fmojournal.fizmatsspu.sumy.ua/publ/3-1-0-93
- Сосницька, Н. Л. (2001). ЗАСОБИ РЕАЛІЗАЦІЇ НОВИХ ПЕДАГОГІЧНИХ ТЕХНОЛОГІЙ У НАВЧАЛЬНОМУ ПРОЦЕСІ З ФІЗИКИ. Наукові записки. Серія: Педагогічні науки, 34, 236-241.
- Чорнобай, К. Г. (2014). МОДЕЛЮВАННЯ ФІЗИЧНОЇ СИТУАЦІЇ ПРИ ФОРМУВАННІ ПРАКТИЧНОЇ КОМПЕТЕНТНОСТІ УЧНІВ З РОЗВ’ЯЗУВАННЯ ФІЗИЧНИХ ЗАДАЧ. Наукові записки. Серія: проблеми методики фізико-математичної і технологічної освіти, 5(1), 179-184.
